Unlike linear data structures (arrays, linked list, queues, stacks, etc.) which have only one logical way to traverse them but trees can be traversed in different ways. The following are commonly used methods for traversing trees.
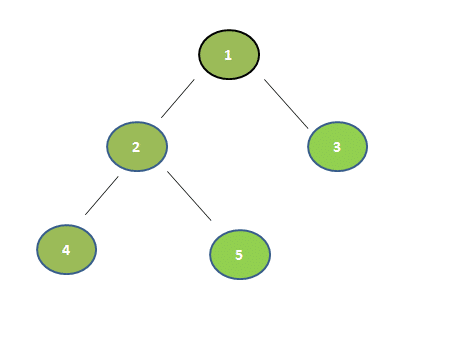
In-order Traversal of above tree (Left, Root, Right) : 4 2 5 1 3
In-order Traversal Steps:
1. Traverse the left subtree, i.e., call Inorder(left-subtree) 2. Visit the root. 3. Traverse the right subtree, i.e., call Inorder(right-subtree)
Example – Program to traverse a tree in In-Order without Recursion
import java.util.Stack;
public class InOrderTraversal {
public static void main(String[] args) throws Exception {
Tree bt = new Tree();
Tree.TreeNode root = new Tree.TreeNode("1");
bt.root = root;
bt.root.left = new Tree.TreeNode("2");
bt.root.left.left = new Tree.TreeNode("4");
bt.root.left.right = new Tree.TreeNode("5");
bt.root.right = new Tree.TreeNode("3");
bt.inOrderWithoutRecursion();
}
}
class Tree {
static class TreeNode {
String data;
TreeNode left, right;
TreeNode(String value) {
this.data = value;
left = right = null;
}
boolean isLeaf() {
return left == null ? right == null : false;
}
}
TreeNode root;
public void inOrderWithoutRecursion() {
Stack<TreeNode> nodes = new Stack<TreeNode>();
TreeNode current = root;
while (!nodes.isEmpty() || current != null) {
if (current != null) {
nodes.push(current);
current = current.left;
} else {
TreeNode node = nodes.pop();
System.out.printf("%s ", node.data);
current = node.right;
}
}
}
}
Output
4 2 5 1 3